Guia de Análise Estatística para Alta Maturidade
Baseline de contratação inicial
Objetivo: Desenvolver, validar e estabelecer uma linha de base quantitativa para um processo capaz de prever a quantidade de dias necessária para a seleção de funcionários, a fim de apoiar a gestão proativa de contratos de alocação de mão de obra no quesito da contratação inicial.
| O objetivo da Baseline é determinar o número de dias necessários para a seleção, e não o tempo para contratação. A seleção é o momento em que o candidato é aprovado pelo entrevistador. Escolhemos não usar os dias necessários para contratação, pois após a seleção temos passos como documentação, aprovação do cliente que tem uma variação muito grande. Além disso, após a seleção, o candidato é enviado ao cliente e o prazo contratual se encerra. |
| Essa baseline deve ser utilizada para as contratações iniciais e no caso de termo aditivo que altera o número de funcionários solicitado pelo cliente. |
Análise Inicial e Prototipagem do Modelo
Foram testados dois modelos de predição:
-
Árvore de decisão
-
Regressão Linear Múltipla
- Modelo de Árvore de Decisão
-
A importância da variável (feature_importances_) é medida pela sua contribuição para a redução da impureza (erro) em cada divisão da árvore. É uma medida contextual e não-linear, que pode mudar quando outras variáveis são adicionadas ou removidas.
- Modelo de Regressão Linear Múltipla
-
A importância da variável é expressa pelos seus coeficientes. Cada coeficiente representa o impacto direto e linear de uma unidade de mudança na variável preditora sobre a variável de destino, mantendo todas as outras constantes.
As métricas de avaliação de resultado dos modelos são o MSE (Mean Square Error) e o MAE (Mean Absolute Error,) pois fornecem perspectivas complementares sobre o erro do modelo. A distinção entre elas foi fundamental para a análise, especialmente no tratamento de outliers.
MAE (Erro Absoluto Médio):
O MAE calcula a média do erro absoluto, dando o mesmo peso a todos os erros.
Vantagem: É mais robusto a outliers e fornece uma medida do erro mais intuitiva, representando o desvio médio real do modelo. A queda brusca do MAE após o tratamento de outliers confirmou que eles distorciam significativamente a média do erro.
MSE (Erro Quadrático Médio):
O MSE calcula a média do erro quadrado.
Vantagem: O MSE penaliza erros maiores de forma mais acentuada. É útil quando grandes desvios da previsão são particularmente indesejáveis.
A análise conjunta do MAE e do MSE é crucial. O MAE nos deu uma visão realista do erro médio do modelo, enquanto o MSE destacou a presença e o impacto de erros significativos, orientando a remoção dos outliers.
Para o teste utilizamos dados históricos de contratação de janeiro de 2024 a dezembro de 2024. Analisando os dados encontramos presença de 6 outliers com valores acima de 50 dias. Para melhorar a estabilidade e a precisão do modelo foi decidido retirar esses outliers.
Por exemplo, no caso da árvore de decisão seguem os erros médios encontrados:
Antes da Remoção dos Outliers:
-
MSE: 157.42629828958047
-
MAE: 8.663780663780665
Após a Remoção dos Outliers:
-
MSE: 67.80485110347146
-
MAE: 6.262826236263735
As implicações da retirada dos outliers são:
- Melhora na Precisão
-
A remoção dos outliers resultou em um modelo com previsões mais precisas e confiáveis.
- Redução do Impacto de Valores Extremos
-
O modelo agora é menos sensível a valores extremos, o que é importante para a estabilidade e a generalização do modelo.
- Modelo Mais Confiável
-
Com a redução dos erros, o modelo se torna mais confiável para prever o tempo de seleção.
Uma etapa crucial na seleção do modelo preditivo é entender como a "importância" de uma variável é definida em diferentes algoritmos.
A Regressão Linear Múltipla oferece uma interpretação direta da influência de cada variável, enquanto a Árvore de Decisão, embora menos interpretável, tende a capturar melhor as relações não-lineares e interações complexas entre as variáveis. O fato de a Árvore de Decisão ter alcançado um desempenho superior em termos de métricas, pois as relações entre os dados não são estritamente lineares.
Otimização do Processo via Engenharia de Atributos de Hiper-parâmetros
Seleção de Atributos (Feature Selection)
A análise de importância das variáveis no modelo de Árvore de Decisão revelou que a variável presencial possuía uma contribuição insignificante.
A remoção desta variável simplificou o modelo, resultando em uma pequena melhora adicional nas métricas:
-
MSE: 61.07
-
MAE: 6.03
Fase 4: Ajuste de Hiper-parâmetros
Uma busca em grade (Grid Search) foi conduzida para otimizar os hiperparâmetros do modelo de Árvore de Decisão.
A melhor configuração encontrada foi: max_depth: 3, min_samples_leaf: 4, e min_samples_split: 2.
Embora a validação do modelo com os hiperparâmetros ajustados tenha retornado um MSE (63.34) e um MAE (6.23) ligeiramente superiores à fase anterior, a diferença foi insignificante. A principal contribuição desta etapa foi confirmar que um modelo mais simples (com profundidade 3) é o ideal para os dados, evitando o overfitting.
Validação Final e Definição da PPB
Com base nesta validação final, a Linha de Base de Performance (PPB) oficial do processo foi estabelecida:
Modelo Selecionado: Arvóre de decisão.
Erro médio ao quadrado: 5,8 dias
Estabilidade: O modelo opera de forma consistente, com diferenças de predição variando de -2 a +2 dias de margem de erro na predição.
Baseline de acompanhamento
Objetivo: Desenvolver, validar e estabelecer uma linha de base quantitativa para um processo capaz de prever a probabilidade de ausências não planejadas de funcionários, a fim de apoiar a gestão proativa de contratos e equipes, em alinhamento visando a otimização e controle estatístico de processo de gerência de contrato.
Definição do Problema e Abordagem Metodológica
A análise exploratória inicial dos dados revelou que as ausências são eventos raros, com a grande maioria dos registros (mais de 90%) apresentando zero dias de desconto. Diante disso, a abordagem inicial de tentar prever a Percentagem a receber (um problema de regressão) foi descartada por ser estatisticamente instável e de baixo valor prático.
A decisão metodológica foi reformular o problema como uma classificação binária: prever a probabilidade de um funcionário ter ou não ao menos uma ausência em um determinado mês (Teve Ausência, Sim ou Não). Esta abordagem se mostrou mais robusta e diretamente alinhada com a necessidade de negócio de identificar potenciais riscos.
Análise Inicial e Prototipagem do Modelo
Foram testados três modelos de classificação:
-
Regressão Logística
-
Random Forest
-
XGBoost
O teste foi realizando utilizando um conjunto de dados inicial de um ano. Nos testes preliminares, o modelo XGBoost demonstrou a maior capacidade de detecção (Taxa de Detecção/Recall) dos casos de ausência, sendo selecionado como o protótipo para uma fase de validação mais rigorosa.
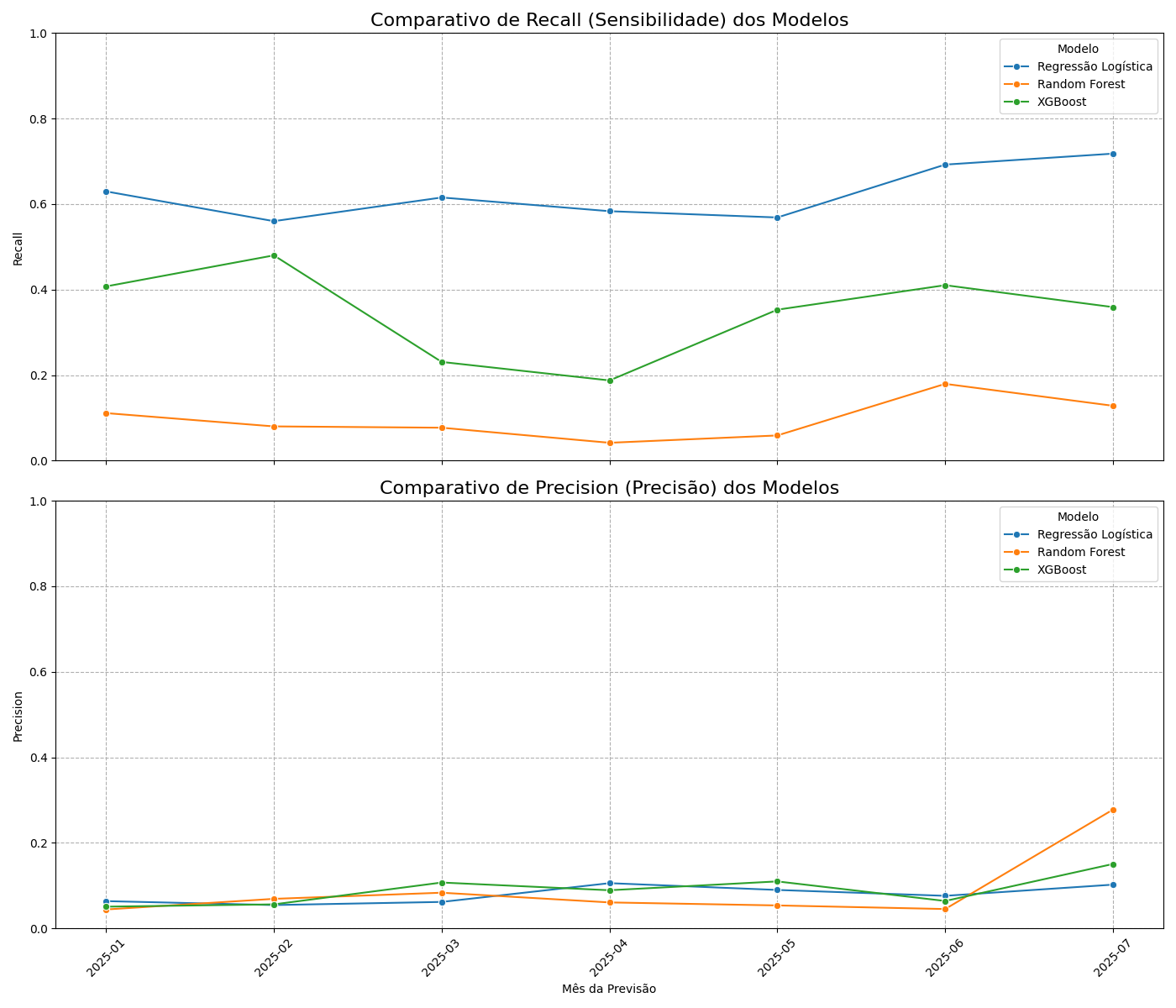
Avaliação Quantitativa e Descoberta de Instabilidade
Para estabelecer uma Linha de Base de Desempenho de Processo (Process Performance Baseline - PPB), foi conduzido um backtest cronológico simulando o desempenho do modelo XGBoost ao longo de 19 meses. Esta análise foi crucial e revelou uma instabilidade significativa no desempenho. A Taxa de Detecção variava drasticamente de um mês para o outro (entre 27% e 92%), indicando que o processo, com as variáveis disponíveis, não estava sob controle estatístico e não era confiável para uso em produção.
Otimização do Processo via Engenharia de Atributos
A causa raiz da instabilidade foi identificada como a falta de variáveis preditivas robustas. O processo foi então otimizado por um extenso trabalho de engenharia de atributos, centralizado no dbt para garantir consistência e governança. O escopo dos dados foi ampliado para três anos (08/2022 a 07/2025) e foram adicionadas novas variáveis-chave, incluindo:
-
Dados de RH: Função (normalizada) e tempo de casa em anos.
-
Dados Contextuais: tamanho da equipe.
-
Dados Comportamentais: O histórico de ausências do próprio funcionário (se ele se ausentou o mês anterior, e o número de ausências nos 3 últimos meses).
Validação Final, Seleção do Modelo e Definição da PPB
Um novo backtest comparativo foi executado com o conjunto de dados enriquecido. Os resultados demonstraram, de forma conclusiva a superioridade do modelo de Regressão Logística. O modelo mais simples, quando alimentado com dados de alta qualidade, provou ser não apenas o de melhor desempenho, mas também o mais estável.
Com base nesta validação final, a Linha de Base de Performance (PPB) oficial do processo foi estabelecida:
Modelo Selecionado: Regressão Logística.
Taxa de Detecção (Recall) Média: 62%.
Estabilidade: O modelo opera de forma consistente, com o recall variando em uma faixa controlada de 56% a 72%, uma melhora drástica em relação aos testes iniciais. Isso pode ser visto no gráfico acima.